Euler

Hoy Google ha dedicado el doodle al gran matemático Leonhard Euler. En Google no hace falta que sea un número redondo de años para celebrar un aniversario y hoy hacía 306 años que nació Euler.
Creo que no hace falta haber estudiado ciencias para que te suene el nombre de este genio del siglo XVIII. Pero si en vez de considerar su nombre tenemos en cuenta sus trabajos y descubrimientos, nos daríamos cuenta de que nuestra vida está plagada de los resultados de su trabajo que fue prolífico y polifacético.
Mi amigo Juan Miguel Suay, Ingeniero, Técnico de Indendios y constructor de cometas, que acaba de leer su tesis doctoral, es un gran admirador de Euler, hasta el punto de que ha usado su nombre como apodo en algunas redes sociales. Hoy apuntaba en su página de Facebook las claves de los elementos presentes en el doodle:

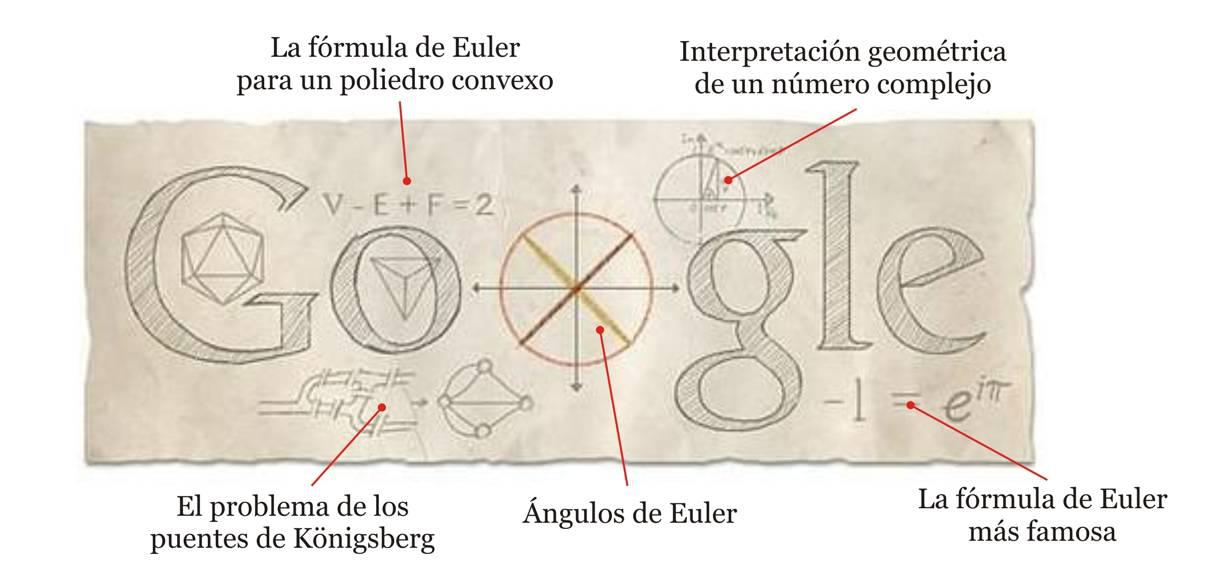
En el interior de la ‘G’ y de la ‘o’ aparecen dos poliedros regulares, el icosaedro es un poliedro de veinte caras triangulares, Para que nos entendamos, se trata de dos pirámides pentagonales, es decir la base es un pentágono y las ‘paredes’, triángulos. Colocadas ambas pirámides enfrentadas por su base, los dos pentágonos que forman las bases se unen por triángulos formados por la arista de un pentágono como base y un vértice del otro pentágono. Como todas las aristas y los ángulos que forman las caras son iguales, es un poliedro regular de los llamados ‘sólidos platónicos’. El otro poliedro es un tetraedro, el más sencillo de los poliedros regulares, formado por cuatro triángulos equiláteros. También podríamos decir que es una pirámide triangular y el poliedro regular más sencillo.
Juan Miguel le tiene mucho cariño al tetraedro pues una de sus cometas favoritas es la cometa de células tetraédricas para construir la cual desarrolló un sistema fácil y rápido uniendo palillos de brocheta con cinta aislante.
Sobre estas figuras aparece una fórmula del teorema de los poliedros: El número de vértices, menos el número de aristas (edges) más el número de caras (faces) es igual a dos. Esta propiedad la cumplen todos los poliedros convexos.
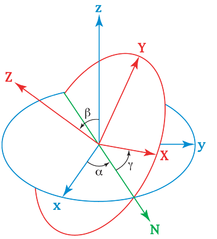En el lugar de la segunda ‘o’ vemos un artilugio que da vueltas cuando pasamos el cursor por encima. Representa otra de las aportaciones de Euler a la ciencia, Los ángulos de Euler, un conjunto de tres coordenadas angulares que sirven para especificar la orientación de un sistema de referencia de ejes ortogonales, normalmente móvil, respecto a otro sistema de referencia de ejes ortogonales normalmente fijos. Esta herramienta clave en el estudio de los movimientos relativos es de suma importancia en la navegación y la astronomía entre otras aplicaciones científicas. Hay que pensar que vivimos en la tierra, un sólido en movimiento, desde el que observamos a los otros astros moverse, por ello. la comprensión de los movimientos relativos es fundamental para el estudio del universo.
La interpretación geométrica de los números complejos nos permite situar a estos en un plano, de la misma forma que los números reales formaban una recta. En la representación, situada sobre la ‘g’ interviene también el número ‘e’, una de las grandes aportaciones de este genio inconmensurable a la ciencia matemática.
Las matemáticas han tenido con frecuencia ‘mala prensa’ porque en el colegio nos las presentaban como un sinfin de cálculos y fórmilas sin relacion con la vida real, pero las matemáticas describen la vida y son una fuente inagotable de divertidas curiosidades. Del numero e podríamos decir que es la base de los logaritmos neperianos, pero en realidad creo que lo más interesante qu puede decirse de él es algo así como lo que nos cuneta la Wikipedia:

, describe el comportamiento de acontecimientos físicos regidos por leyes sencillas, como pueden ser la velocidad de vaciado de un depósito de agua, el giro de una veleta frente a una ráfaga de viento, el movimiento del sistema de amortiguación de un automóvil o el cimbreo de un edificio metálico en caso de terremoto. De la misma manera, aparece en muchos otros campos de la ciencia y la técnica, describiendo fenómenos eléctricos y electrónicos (descarga de un condensador, amplificación de corrientes en transistores BJT, etc.), biológicos (crecimiento de células, etc.), químicos (concentración de iones, periodos de semidesintegración, etc.), y muchos más.

Asi podemos comprender porque al número e se le ha llamado el número de la naturaleza. ¿Como puede ser que tantos fenómenos naturales tengan como componente común una constante de curiosas propiedades, como el numero ‘Pi’ en la geometria, el número ‘e’ es considerado el número por excelencia del cálculo y conocido a veces como número de Euler o constante de Napier, un sabio escocés, primero en usar los logaritmos.
el problema de los puentes de Königsberg, resuelto por Euler dando origen a la teoría de grafos.
La cuestión es que a partir de un problema de ingenio sobre la posibilidad de hacer un recorrido por la ciudad pasando solo una vez por cada puente y acabando en el mismo sitio que s enmpezó, Euler desarrolló no solo una solución al problema sino un método general para el estudio de problemas de este tipo que sigue siendo una herramienta fundamental en la solución de todo tipo de problemas y que tiene aplicación en cuestiones tan cotidianas como las orientaciones que nos da nuestro GPS para llevarnos al destino elegido.
Por último, bajo la letra ‘e’ en el doodle aparece la Identidad de Euler, quizás su fórmula más famosa, por relacionar cinco números muy utilizados en la historia de las matemáticas y que pertenecen a distintas ramas de la misma.
Y estas son las referencias que hace Google al trabajo y la vida de Euler. Pero son solo una pequeña muestra de su aportación al conocimiento. Su excepcional inteligencia produjo unas obras completas que reunidas podrían ocupar entre 60 y 80 volúmenes, publicando un promedio de 800 páginas de artículos al año en su época de mayor producción, entre 1727 y 1783.
Otras grandes aportaciones a la ciencia fueron el concepto de función, siendo el primero en usar la notación f(x), la notación moderna de las funciones trigonométricas, la letra griega ∑ (sigma) como representación de sumatorios, y popularizó el uso de ‘pi’, aunque no fue su inventor. Sus trabajos en la Teoria de números, Astronomía y física (incluido un estudio sobre el vuelo de las cometas), la lógica o la arquitectura y la ingeniería le convierten en uno de los sabios más influyentes de la historia sin cuyas aportaciones nuestro mundo sería muy diferente de como es.